Have you ever entered a city and thought “what gave this city its form? What is its purpose?” At first glance, it appears to be a consequence of demographic movements: people living, working, and playing, keeping the wheels of society moving. Look a bit deeper, however, and the question remains unresolved: the organization of every aspect of the city, from its workers to the buildings that give it form, were shaped by the forces that set the wheels in motion to begin with. These forces are represented by such names as Starbucks, Microsoft, and J.P. Morgan, to name only a few, but behind each of these businesses is a guiding principle and motive force: an idea. And underlying each of the ideas, the missions, that form the core operating philosophy of each business are the ideas of capitalism and trade. Thus, the city is much more than a collection of buildings: for better or for worse, it is the stamp of a collection of expressly man-made ideas upon reality.

Universality refers to two central principles of Panidealism. The first is theoretical: it states that reality can be described in terms (or even stronger, is in fact composed) of combinations of simple constituent ideas. The second principle is an applied corollary of the first: that one can gain insight into new ideas by studying existing ideas (primarily through the processes of inductive and analogical reasoning), since the overlapping constituent ideas will only require comprehension once. We can ineluctably conclude from these two principles that breadth has an essential role in the process of quickly learning, integrating, and applying new ideas. Moreover, examination of the ideas common to all fields from many different perspectives yields fundamental insight into the nature of ideas themselves, structured systems, and the fundamental concept of Beauty.

When we refer to “ideas” in this sense, we are not speaking solely of ideas realized in our minds. Certainly these ideas are included, but the qualities that make natural (and man-made, or even abstract) objects appear as they do to our senses and mind also constitute ideas. In this sense, they resemble the Forms of Plato: a tree is an idea, as we can speak of something as a tree and immediately form a mental picture of what it is. However, we do not speak of ideas as inhabiting some abstract realm, as Plato, neither do we consider them inherent in the nature of the objects they describe as they appear to our senses, as Aristotle. Rather, we hold that ideas retain an objective meaning within reality (and not some abstract realm) that is paradoxically inestimable by our senses because we hold an incomplete set of knowledge about the world. The appearance of the idea to the mind may be very different from the objective meaning of the idea; only ideas remaining entirely within the mind of a solitary creator are ascribed a single abstract meaning (since the objective meaning is the subjective meaning in this circumstance). For example, music is an idea that takes on both concrete forms (sound waves, notes printed on a page, certain motions of the fingers on a piano, …) and yet possesses an abstract meaning at a higher level than all of these things (after all, they're all considered “music”). Say we take a Beethoven piece as an example. When the music existed solely within Beethoven's mind, it had a single abstract meaning - his own. Once it was written down, it acquired a canonical representation outside of Beethoven's mind: notes on a page, phrased in a language interpretable by a musician. Any competent musician, however, will not play solely the expressions indicated on the page. Rather, he will put his “feeling” into his rendition of the piece, taking care to make sure it sounds “like Beethoven music”. Even though such a set of ideas surely exists, we would be hard pressed to identify what makes a piece “like Beethoven music” (or, for that matter, “music” at all), and we would get different answers from different people if we asked.

Ideas also exist in timelines that may be independent of the objects they realize. For example, a scene in nature exists before it is photographed, even though we may only know of the underlying scene from the photograph. Conversely, ideas may be conceptualized in such media as science fiction novels today, but may not be truly realized in reality for a long time, if ever.

The mathematical intuition underpinning this philosophy comes from the idea of bases and images in linear algebra (and is thus a perfect example of this principle in action). Perhaps they can also be referred to as the philosophical concepts of extension and intension. Informally, we define the image of a matrix as the set of all possible linear combinations of its columns; that is, all possible ways in which the vectors can be multiplied by scalars and summed. The basis of a matrix is then the smallest set of columns that contains the same image as the full matrix. Equivalently, we can define it as the largest set of columns in the matrix that contains no redundancies (that is, the set of columns we can't by multiplying other columns by any number and/or adding them). The number of such columns (which is always equal to the number of such rows) is called the rank of the matrix. For example,

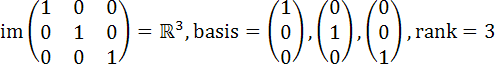
The image of this matrix (called the 3-dimensional identity matrix, or simply I³) is all of 3-space (R³), since each column represents one dimension, while the basis is just the set of individual vectors (since the matrix contains no column redundancies). Thus, the corresponding rank is 3.

We may now simply speak of the set of ideas underlying a thing as its basis and the total sum of the thing's implications and relations as the image of those ideas. Because the image of both the original matrix and the basis remain the same, it is theoretically possible to mentally decompose the reality of an object into its constituent basis of ideas, intuitively removing the redundancies without losing any information. Because the image remains the same, none of the implications or value of the idea is lost. While this is possible in theory, it becomes intractable in practice, since even a finite basis has an infinite set of implicit ideas! We may imagine many objects that express the concept of “tall”, for example, but we can always imagine something taller! For every integer n, we can imagine a greater integer n+1, and if we consider the reals, there are an infinitude of numbers just between 1 and 2! This intractability is central to the principle of subjectivity, which is discussed in a separate article.

Abandoning the abstract mathematical formalism for something more concrete, let us take the example of a tree. Some ideas that make up our mental image of a tree are “made of wood”, “branches”, and “photosynthetic”. These are just a few; naming all such properties that make up the concept of a tree is impossible. Clearly, not everything that is made of wood is a tree (baseball bat?), nor is everything photosynthetic a tree (algae?), nor would any single nonreflexive idea qualify an object to be called a tree. However, it is the combination of these ideas that allows us to instantly recognize an object as a tree. We can represent this as the image of the “tree” concept, as shown below:

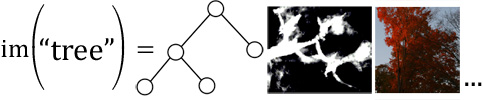
Now suppose that someone trained in computer science recognizes a tree. Due to his training in the concept of abstract trees, he may realize that the branching topology of a real tree may be largely represented by an abstract tree (because both types have the redundant idea of “branches”). Alone, we now have a concise representation for encoding trees, with instruction in one discipline required. However, if we also have training in anatomy or radiology, we may recognize the second image above as an example of a medical tree-like structure (because it too branches).

By combining insights from our computational and medical training, we should be able to realize that it is possible to capture the branching properties of this anatomical structure with an abstract tree. This is essentially a decomposition of the “tree” idea into “something that branches” and the joining of two distinct applications that have this idea in common. This is useful because (as someone with medical training would know) certain diseases, such as cancer, can affect the structure of parenchymal trees, causing them to become distorted and thus causing the abstract representation to change. This ends up leading to the creation of a powerful tool for medical diagnosis, which we have actually implemented. Our current version computationally detects radiological findings with 86% accuracy. This is just a small (two-discipline) example of what can be accomplished using the insights gained from the fusion of multiple classical disciplines - a consequence of the principle of Universality.

On Communities

Defining reality as a particular expression of an idealistic basis has additional implications, however: in keeping with Panidealism as a primarily individualistic philosophy, universality also allows individuals to do things that communities cannot (in fact, this may also be the root cause of some of the purely empirical observations of objectivism). Returning to our mathematical formalism, recall that the rank of a matrix is the number of independent columns (which is always equal to the number of independent rows). While the rank defines the number of non-redundant rows/columns in the matrix, the number of remaining rows/columns is the nullity of the matrix, or dimensionality of the matrix's null-space (the space that maps to zero). Formally, we can simply state that the rank and nullity add to the number of columns in the matrix. That is, if A is a matrix with c columns,

rank(A) + nullity(A) = c

(The Rank-Nullity Theorem)

This is important because the null-space maps all inputs to the same output (0); it is entirely redundant. Thus, the null-space consists of ideas that quite literally add nothing. The rank of a concept therefore quantifies the ability to derive new ideas from that concept.

Now, rather than discussing trees and vectors (there is nothing contradictory about a tree since it is able to exist in reality, thus its nullity, as of any object that is physically present, should be small or even zero. The nullity of the vector is clearly 0 as well, corresponding to a null-space of only a single point, since only (0,0,0) maps to 0), let's consider individuals and communities. New ideas are derived from existing ideas present in the concept of an entity's cognition. Redundancies and contradictions can indeed exist in the mind, so the nullity of thought can potentially be very high. The corresponding low rank indicates that many of the ideas held in a mind may contribute no value to the generation of new ideas; thus, the higher the rank, the more ideas a person may draw on.

Now to the heart of the argument: this applies to communities as well. Communities are groups of people, each contributing their own ideas. However, many of these ideas will be redundant - the community's rank will be far lower than the sum of the ranks of its individual members. Moreover, existing members of a community tend to select new members on the basis of similarity to a desired ideal. While this manner of selection seems desirable, great caution must be exercised to vary the selection criteria sufficiently, for as the community size grows, its rank, and thus its ability to generate new ideas, must keep up with the expenses of maintaining a larger community, such as increased overhead of communication. A community that fixes static criteria for its members will ultimately find itself with idea generating power comparable to or even less than that of a single individual. Since most people share the majority of their ideas and value systems, this is the most likely outcome as a community grows larger even in absence of deliberate selection for it, and explains why individuals can often innovate in ways that entire organizations cannot. Proficiency-oriented measures are less susceptible to this than value-oriented measures, as proficiency can be attained through many distinct paths and the added ability to implement ideas may compensate for the inability to generate new ones, but even organizations such as competitive companies and universities attempt to recruit on the basis of things such as “fit” - a major mistake, as it ensures precisely the sort of homogeneity that will be their downfall. Just as many instruments playing in unison add to the strength of a single harmonic voice but fail to contribute any new harmony, simply adding people with similar ideas strengthens the momentum but not the vision of a community. This too is a consequence of Universality.

(It should be noted that this is an argument for diversity of ideas, which is a completely orthogonal concept to race, gender, or skin color).

On Polymaths

Finally, the principle of universality provides a theoretical reason to acquire a broad knowledge base. The set of ideas any one person can hold is infinitesimally small compared to the sum total of human knowledge. This view is expressed by Socrates in his famous statement that “he is the wisest of men because he knows nothing”, but all that is required to see this is a walk into a moderately-sized library. However, what is important is not how much one knows, but how much one can learn if necessary. This is quite simply the image of one's acquired knowledge. Since we have shown that the rank of one's knowledge base corresponds to the number of non-redundant ideas one holds, the easiest way to increase the size of this image is to acquire diverse ideas from many different disciplines.

Thus, the principle of universality forms a motivation for the training of polymaths.